Предположим, что враг загнал вас в угол и вам грозит верная смерть. И что у вас есть право на последнее желание. На этот случай у нас есть прекрасная идея: попросите вашего врага решить головоломку ДиЛанда — и вы займёте его надолго, так надолго, что вполне возможно, он успеет забыть о ваших разногласиях.
Парадокс чародея-любителя Теодора ДиЛанда — вариант головоломки, известной как «недостающий квадрат». Суть у них одна: существует определённое количество объектов; при простой перестановке этих объектов один из них бесследно исчезает — непонятно куда и как.
Вот пример с вышеупомянутым недостающим квадратом: 4 фрагмента треугольника просто меняются местами, при этом размер треугольника остаётся тем же, но одна клетка оказывается пустой. Как так?
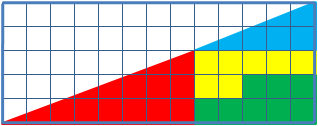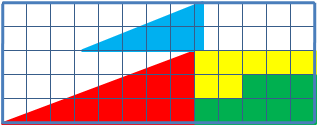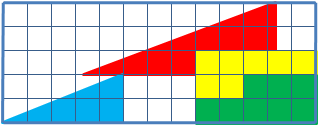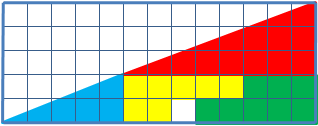
А вот пример ДиЛанда с картами. Было 16, при перестановке осталось 15. Сможете догадаться, как это произошло?

И, наконец, человечки — было 12, стало 13. Куда при перестановке пропадает один из них и откуда снова появляется?
Решение:
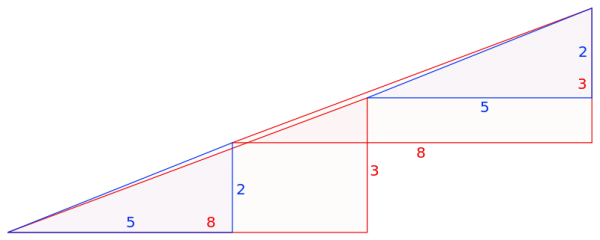
Для начала разберёмся с треугольником. Дело в ошибке, замаскированной в самом условии задачи. Площади переставляемых фигур, разумеется, не меняются. Но при ближайшем рассмотрении оказывается, что гипотенуза большого треугольника слегка искривлена — в одном случае внутрь, а при перестановке получается, что наружу. За счёт этого во втором случае и образуется «лишняя площадь».
С картами и человечками принцип один и тот же: Объекты расположены в определённых интервалах друг от друга. При перестановке один фрагмент от каждого объекта переходит к следующему, и из этих «кусочков» создаётся новый объект. Вот так просто.
Теперь, если есть время, попробуйте вернуться и разглядеть, как это происходит.
http://mixstuff.ru/
Парадокс чародея-любителя Теодора ДиЛанда — вариант головоломки, известной как «недостающий квадрат». Суть у них одна: существует определённое количество объектов; при простой перестановке этих объектов один из них бесследно исчезает — непонятно куда и как.
Вот пример с вышеупомянутым недостающим квадратом: 4 фрагмента треугольника просто меняются местами, при этом размер треугольника остаётся тем же, но одна клетка оказывается пустой. Как так?

А вот пример ДиЛанда с картами. Было 16, при перестановке осталось 15. Сможете догадаться, как это произошло?

И, наконец, человечки — было 12, стало 13. Куда при перестановке пропадает один из них и откуда снова появляется?
Решение:
Для начала разберёмся с треугольником. Дело в ошибке, замаскированной в самом условии задачи. Площади переставляемых фигур, разумеется, не меняются. Но при ближайшем рассмотрении оказывается, что гипотенуза большого треугольника слегка искривлена — в одном случае внутрь, а при перестановке получается, что наружу. За счёт этого во втором случае и образуется «лишняя площадь».

С картами и человечками принцип один и тот же: Объекты расположены в определённых интервалах друг от друга. При перестановке один фрагмент от каждого объекта переходит к следующему, и из этих «кусочков» создаётся новый объект. Вот так просто.
Теперь, если есть время, попробуйте вернуться и разглядеть, как это происходит.
http://mixstuff.ru/


[ Регистрация | Вход ]